Vidas desiguais na cidade de São Paulo
Identificamos quais as contribuições de cada causa de morte para a diferença de 24 anos entre expectativas de vida em diferentes distritos da cidade de São Paulo.

Introdução
Em 2017, a rede Nossa São Paulo publicou um mapa da desigualdade comparando os diferentes distritos da cidade de São Paulo em termos de diversos indicadores sociais. Uma das desigualdades encontradas foi a diferença estarrecedora de quase 24 anos entre as expectativas de vida dos distritos melhor e pior colocados (79,4 anos no Jardim Paulista e 55,70 no Jardim Ângela). Meu objetivo nesta análise foi discriminar como as diferentes causas de morte contribuem para essa diferença, atribuindo um "número de anos subtraídos" a cada uma. A metodologia utilizada é apresentada logo abaixo do resultado principal, seguida de outros resultados interessantes descobertos durante a análise dos dados. Este estudo foi publicado na revista Le Monde Diplomatique Brasil.
Resultado principal
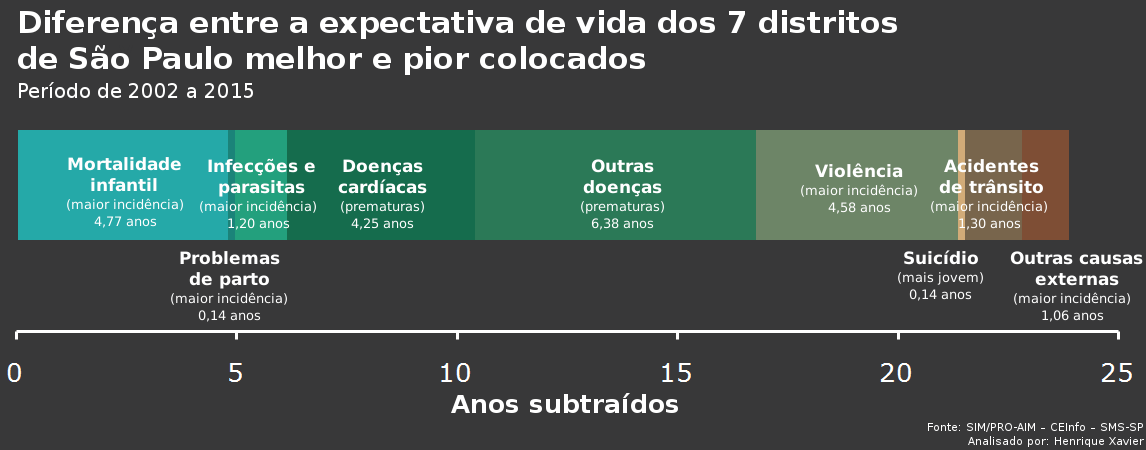
Para reduzir flutuações estatísticas, contabilizamos os óbitos ocorridos no período de 2002 a 2015 e criamos um grupo dos sete distritos com expectativa de vida mais alta (Alto de Pinheiros, Consolação, Itaim Bibi, Jardim Paulista, Moema, Pinheiros e Vila Mariana, que chamaremos de "bairros ricos") e outro dos sete com expectativa de vida mais baixa (Anhanguera, Cidade Tiradentes, Grajaú, Iguatemi, Jardim Ângela, Parelheiros e São Rafael, que chamaremos de "bairros pobres"). Para cada causa de morte no grupo de expectativa mais baixa, calculamos qual seria o acréscimo na expectativa de vida se tais falecimentos fossem alterados para o patamar observado no grupo de maior expectativa de vida (os bairros ricos). O resultado final pode ser visto na figura acima. O comprimento da barra colorida representa a diferença em anos entre as expectativas de vida dos bairros ricos e dos bairros pobres, que pode ser comparado à escala na parte inferior da figura. A barra é segmentada de acordo com as contribuições associadas a cada causa mortis. Por exemplo, maior incidência de violência nos bairros pobres reduz a expectativa de vida em 4,58 anos em relação aos bairros ricos, enquanto que a incidência prematura (ou seja, levando a óbito em idades mais baixas) de doenças cardíacas nos bairros pobres resulta em 4,25 anos a menos de vida, em média, quando comparado aos bairros ricos. Ao final, levando em conta todas as causas, a diferença total na expectativa de vida é de 23,8 anos.
O conjunto denominado Mortalidade infantil corresponde a todos os óbitos (por qualquer causa)
de pessoas com idade inferior a um ano; a fração dos óbitos que ocorrem nessa idade é 7,4 vezes maior nos
bairros pobres quando comparada aos bairros ricos. No cálculo da contribuição das demais causas para a diferença
na expectativa de vida, consideramos apenas óbitos com idade de um ano ou mais. Para essas causas,
temos as seguintes correspondências com os capítulos da Classificação Internacional de Doenças (CID):
Problemas de parto: Cap. 15 (que inclui problemas na gravidez),
cuja fração do total de óbitos é 11 vezes maior nos bairros pobres;
Infecções e parasitas: Cap. 1, cuja fração do total de óbitos é 85% maior nos bairros pobres;
Doenças cardíacas: Cap. 9, cujos óbitos decorrentes dessa causa acontecem tipicamente mais cedo
nos bairros pobres em relação aos bairros ricos;
 Outras doenças: Caps. 2 a 18, com exceção dos Caps. 9 e 15 já listados,
que também causam óbitos mais cedo nos bairros
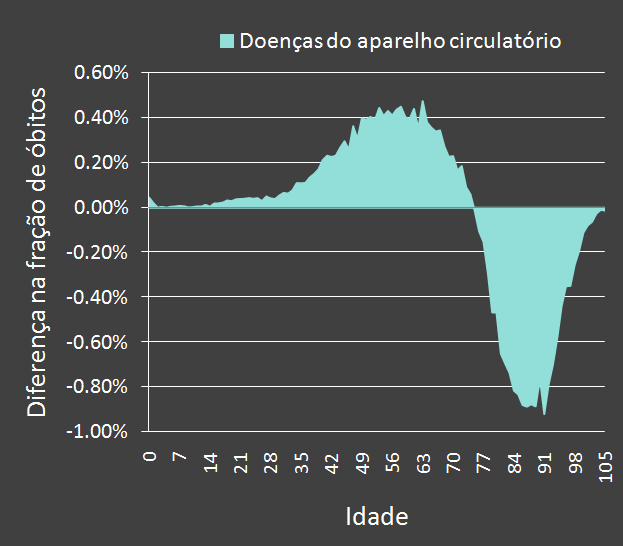
mais pobres. Para exemplificar a diferença entre as distribuições de óbitos por idade dos bairros pobres e dos
bairros ricos no contexto de causas que acarretam em óbitos prematuros nestes últimos,
apresentamos ao lado o gráfico da
diferença entre as frações de óbitos ocorridos por doenças cardíacas. Podemos notar que, embora o óbito por esse
tipo de doença seja aproximadamente igual nos dois grupos, ele acomete os bairros ricos preferencialmente em idades mais
altas.
Outras doenças: Caps. 2 a 18, com exceção dos Caps. 9 e 15 já listados,
que também causam óbitos mais cedo nos bairros
mais pobres. Para exemplificar a diferença entre as distribuições de óbitos por idade dos bairros pobres e dos
bairros ricos no contexto de causas que acarretam em óbitos prematuros nestes últimos,
apresentamos ao lado o gráfico da
diferença entre as frações de óbitos ocorridos por doenças cardíacas. Podemos notar que, embora o óbito por esse
tipo de doença seja aproximadamente igual nos dois grupos, ele acomete os bairros ricos preferencialmente em idades mais
altas.
As demais causas apresentadas na primeira figura são classificadas como "Causas Externas" (Cap. 20) e foram subdivididas em: Violência, que inclui os óbitos classificados como "homicídio", "lesões de intenção indeterminada" e "intervenção legal", cada um contribuindo com 3,93, 0,49 e 0,16 anos de diferença na expectativa de vida e com frações do total de óbitos 13,6, 3,2 e 9,5 vezes maior nos bairros pobres, respectivamente; Suicídio, afetando pessoas em idades tipicamente mais baixas em bairros pobres; Acidentes de trânsito, que inclui "Atropelamento de pedestre", "Ciclista traumatizado em acidente de transporte", "Motociciclista traumatizado em acidente de transporte" e "Demais acidentes de trânsito e transporte", cada um contribuindo com 0,40, 0,05, 0,49, e 0,36 anos de diferença na expectativa de vida e com frações do total de óbitos 3,3, 3,4, 7,4 e 2,4 vezes maior nos bairros pobres, respectivamente; e Outras causas externas, que inclui "Queda acidental", "Afogamento acidental", "Choque elétrico acidental", "Exposição a fogo acidental" e outros, todos com maior frequência para residentes em bairros pobres. Hipotetizamos que parte dessa maior incidência de mortes acidentais entre residentes de bairros pobres decorra do fato de que profissões perigosas (motoboys, trabalhadores da construção civil, entre outras) são, em geral, ocupadas por pessoas pobres.
Metodologia
 Para poder discriminar a quantidade de anos que cada causa mortis contribui para a diferença na expectativa
de vida, é necessário supor como as pessoas viriam a falecer caso não fossem acometidas pela causa e na idade
em questão. Como queremos comparar as expectativas de vida de dois grupos, nossa solução foi a seguinte: nós
tomamos a distribuição dos bairros ricos como referência (cuja incidência de qualquer causa mortis ou é mais
baixa ou ataca as pessoas em idades tipicamente mais avançadas do que nos bairros pobres) e assumimos que
residentes de bairros pobres acometidos pela causa em questão viriam falecer de acordo com essa distribuição
de referência (que inclui óbitos pela causa tratada, mas em menor quantidade ou em idades mais avançadas).
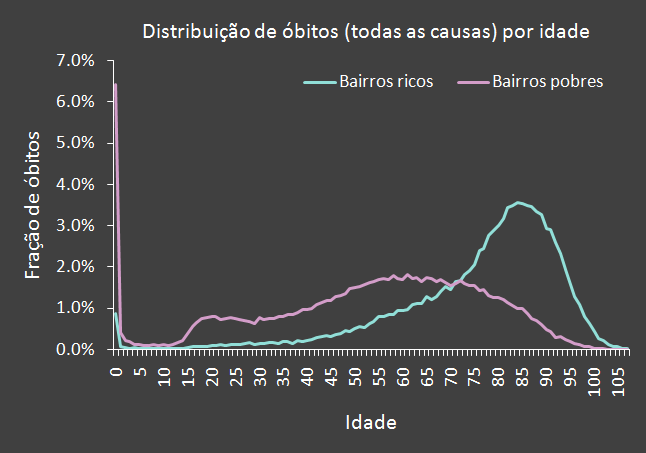
Após esse ajuste, a expectativa de vida é recalculada e a diferença inferida. O gráfico que acompanha este
parágrafo mostra as distribuições por idade dos óbitos de residentes em bairros ricos e bairros pobres, levando
em conta todas as causas. O "degrau" ao redor dos 15 anos observado na distribuição dos bairros pobres
é causado, majoritariamente, pela violência.
Para poder discriminar a quantidade de anos que cada causa mortis contribui para a diferença na expectativa
de vida, é necessário supor como as pessoas viriam a falecer caso não fossem acometidas pela causa e na idade
em questão. Como queremos comparar as expectativas de vida de dois grupos, nossa solução foi a seguinte: nós
tomamos a distribuição dos bairros ricos como referência (cuja incidência de qualquer causa mortis ou é mais
baixa ou ataca as pessoas em idades tipicamente mais avançadas do que nos bairros pobres) e assumimos que
residentes de bairros pobres acometidos pela causa em questão viriam falecer de acordo com essa distribuição
de referência (que inclui óbitos pela causa tratada, mas em menor quantidade ou em idades mais avançadas).
Após esse ajuste, a expectativa de vida é recalculada e a diferença inferida. O gráfico que acompanha este
parágrafo mostra as distribuições por idade dos óbitos de residentes em bairros ricos e bairros pobres, levando
em conta todas as causas. O "degrau" ao redor dos 15 anos observado na distribuição dos bairros pobres
é causado, majoritariamente, pela violência.
Matematicamente, o primeiro passo para a nossa análise foi calcular a distribuição de óbitos \(f_{g,c}(t)\) por causa \(c\) e por idade \(t\) para um grupo \(g\): $$ f_{g,c}(t) = \frac{N_{g,c}(t)}{N_{g,\mathrm{tot}}}. $$ Em português: para um dado grupo, nós dividimos o número de mortes em cada idade e em cada causa \(N_{g,c}(t)\) pelo total de mortes daquele grupo \(N_{g,\mathrm{tot}}\), o que nos dá a fração de óbitos que aconteceram devido à causa \(c\) e na idade \(t\). A expectativa de vida de um grupo \(\langle t \rangle_g\) pode ser calculada pela multiplicação de \(f_{g,c}(t)\) por \(t\) e sua posterior soma sobre todas as causas e idades: $$ \langle t \rangle_g = \sum_{t,c} t f_{g,c}(t), $$ e a diferença entre a expectativa de vida de dois grupos \(g\) e \(h\), com distribuições \(f_{g,c}(t)\) e \(f_{h,c}(t)\), depende apenas da diferença \(s_{c}(t) \equiv f_{h,c}(t)-f_{g,c}(t)\) entre as distribuições: $$ \langle t \rangle_h - \langle t \rangle_g = \sum_{t,c} t f_{h,c}(t) - \sum_{t,c} t f_{g,c}(t) = \\ = \sum_{t,c} t [f_{h,c}(t) - f_{g,c}(t)] = \sum_{t,c} t s_{c}(t). $$ Note que, pela definição de \(f_{g,c}(t)\), $$ \sum_{t,c} f_{g,c}(t) = 1 $$ (todo mundo morre de alguma coisa em algum dia), e por isso: $$ \sum_{t,c} s_{c}(t) = 0. $$ Isso significa que, se a diferença \(s_{c}(t)\) entre as distribuições de óbitos nos dois grupos fosse zerada para alguma causa \(c_0\) e idade \(t_0\), uma modificação compensatória de mesma magnitude total teria que ser feita nos restante de \(s_{c}(t)\), para todo \(c\neq c_0\) e \(t\neq t_0\). Como dissemos antes, as pessoas viriam a falecer em outras circunstâncias caso não fossem acometidas pela causa \(c_0\) e na idade \(t_0\) em questão.
Para prosseguir, vamos definir \(s^+_{c}(t) \equiv \mathrm{max}[s_{c}(t),0]\) e \(s^-_{c}(t) \equiv \mathrm{min}[s_{c}(t),0]\), ou seja, \(s^+_{c}(t)\) e \(s^-_{c}(t)\) são as diferenças \(s_{c}(t)\) que são positivas e negativas, respectivamente (para as demais \(c\) e \(t\), essas funções são zero). Para estudar a influência de um excesso de óbitos \(s^+_{c_0}(t_0)\) na diferença entre expectativas de vida, \(\Delta \langle t \rangle_{c_0,t_0}\), nós fazemos: $$ \Delta \langle t \rangle_{c_0,t_0} = - t_0 s^+_{c_0}(t_0) + \alpha_{c_0}(t_0) \sum_{c,t} t s^-_{c}(t),$$ $$ \alpha_{c_0}(t_0) \equiv \frac{s^+_{c_0}(t_0)}{\sum_{c,t}s^-_{c}(t)}.$$ O primeiro termo da direita da primeira equação retira a influência do excesso de óbitos com causa e idade específicas \(c_0\) e \(t_0\), enquanto que o segundo termo compensa essa retirada com um aumento de mortes distribuídos em todas as idades e causas na qual existe uma falta de óbitos. O fator que modula essa compensação, \( \alpha_{c_0}(t_0)\), é simplesmente o excesso de probabilidade que foi retirado, dividido pelo total de faltas que vão entrar na compensação (esta última necessária devido à conservação de probabilidade). Ou seja, nós assumimos que as mortes em excesso num grupo, quando anuladas, são igualmente distribuídas entre todas as causas e idades que têm falta de óbitos em relação ao grupo de referência. Para o caso estudado (bairros pobres e bairros ricos), isso significa, por exemplo, transferir óbitos de jovens por violência para uma combinação de óbitos mais tardios causados por neoplasias, doenças cardíacas e outras complicações típicas de idades mais avançadas. Para contabilizar a influência de uma causa \(c_0\) independentemente da idade, basta somar \( \Delta \langle t \rangle_{c_0,t_0}\) sobre \(t_0\).
A planilha de Excel utilizada nessa análise pode ser obtida aqui. Os dados utilizados foram obtidos do Sistema de Informações sobre Mortalidade (SIM). As declarações de óbito que ocorreram no município de São Paulo são processadas pelo Programa de Aprimoramento das Informações de Mortalidade no Município de São Paulo (PRO-AIM). Os dados podem ser acessados aqui.
Outros resultados: pessoas sem endereço
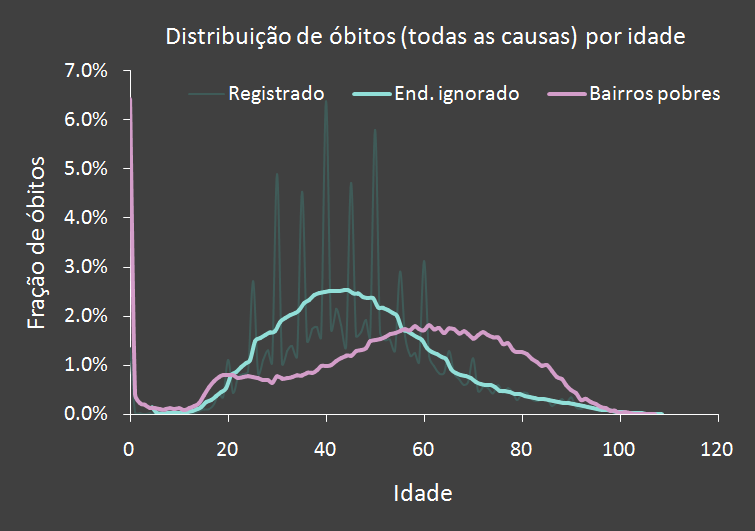 Existe um grupo que apresenta expectativa de vida ainda mais baixa (de 46,2 anos) que a dos residentes
em bairros pobres: as pessoas sem endereço conhecido (registrados nas declarações de óbito com "endereço ignorado").
A figura ao lado compara a distribuição por idade dos óbitos dessas pessoas com a dos residentes em bairros pobres.
Hipotetizamos que essas pessoas estejam em situação de rua ou que não possuam familiares ou outra forma de
identificação. Note que a curva denominada "End. ignorado" trata-se, na verdade, de uma média móvel
(em 10 anos) da curva denominada "Registrado". Esta última é a idade de fato registrada na declaração de óbito,
e apresenta picos em múltiplos de 5 (20, 25, 30, 35 anos...). Nossa hipótese para explicar esses dados é a seguinte:
embora o médico responsável pela declaração de óbito possa registrar "Idade ignorada" (opção bastante frequente
entre as pessoas com endereço ignorado), muitos médicos "chutam" uma idade aproximada; nesse chute, múltiplos de 5
são preferidos, e números "redondos" (20, 30, 40 anos...) são ainda mais. Assumindo que idades vizinhas às preferidas
são realmente conhecidas (e estimando o número de óbitos em idades preferidas cuja idade é de fato conhecida como
a média dos dois vizinhos), podemos estimar a porcentagem de falecidos com idade desconhecida que são registrados
com idade "chutada": aproximadamente 52%, sendo que essa porcentagem varia bastante um função da idade.
Existe um grupo que apresenta expectativa de vida ainda mais baixa (de 46,2 anos) que a dos residentes
em bairros pobres: as pessoas sem endereço conhecido (registrados nas declarações de óbito com "endereço ignorado").
A figura ao lado compara a distribuição por idade dos óbitos dessas pessoas com a dos residentes em bairros pobres.
Hipotetizamos que essas pessoas estejam em situação de rua ou que não possuam familiares ou outra forma de
identificação. Note que a curva denominada "End. ignorado" trata-se, na verdade, de uma média móvel
(em 10 anos) da curva denominada "Registrado". Esta última é a idade de fato registrada na declaração de óbito,
e apresenta picos em múltiplos de 5 (20, 25, 30, 35 anos...). Nossa hipótese para explicar esses dados é a seguinte:
embora o médico responsável pela declaração de óbito possa registrar "Idade ignorada" (opção bastante frequente
entre as pessoas com endereço ignorado), muitos médicos "chutam" uma idade aproximada; nesse chute, múltiplos de 5
são preferidos, e números "redondos" (20, 30, 40 anos...) são ainda mais. Assumindo que idades vizinhas às preferidas
são realmente conhecidas (e estimando o número de óbitos em idades preferidas cuja idade é de fato conhecida como
a média dos dois vizinhos), podemos estimar a porcentagem de falecidos com idade desconhecida que são registrados
com idade "chutada": aproximadamente 52%, sendo que essa porcentagem varia bastante um função da idade.
Outros resultados: aposentadoria
 A distribuição por idade dos óbitos também nos permite comparar os dois grupos em termos
da fração de pessoas que vivem além da idade de aposentadoria \(t_A\). Essa fração \(A_g(t_A)\) para o grupo
\(g\) pode ser calculada pela fórmula:
$$ A_g(t_A) = \sum_{c,t>t_A} f_{g,c}(t) $$
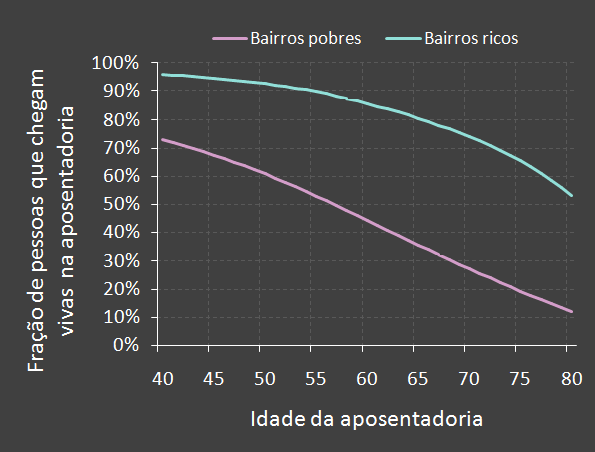
O gráfico do lado mostra essa fração em função da idade de aposentadoria para os bairros ricos e bairros
pobres. Por exemplo, as frações de residentes em bairros ricos que chegam a 55 e a 65 anos são 90% e 80%, enquanto
que as frações para residentes de bairros pobres são 53% e 35%, respectivamente. Embora essas frações levem em conta
óbitos por mortalidade infantil e violência (que atinge especialmente os jovens próximos de 20 anos), a variação no
número de pessoas que atingem a aposentadoria numa eventual mudança na idade da aposentadoria não é afetada por
esses óbitos prematuros. No caso de uma mudança, nos dias de hoje, de 55 para 65 anos, por exemplo, o número de
pessoas que se aposentam diminuiria 11% nos bairros ricos e 34% nos bairros pobres.
A distribuição por idade dos óbitos também nos permite comparar os dois grupos em termos
da fração de pessoas que vivem além da idade de aposentadoria \(t_A\). Essa fração \(A_g(t_A)\) para o grupo
\(g\) pode ser calculada pela fórmula:
$$ A_g(t_A) = \sum_{c,t>t_A} f_{g,c}(t) $$
O gráfico do lado mostra essa fração em função da idade de aposentadoria para os bairros ricos e bairros
pobres. Por exemplo, as frações de residentes em bairros ricos que chegam a 55 e a 65 anos são 90% e 80%, enquanto
que as frações para residentes de bairros pobres são 53% e 35%, respectivamente. Embora essas frações levem em conta
óbitos por mortalidade infantil e violência (que atinge especialmente os jovens próximos de 20 anos), a variação no
número de pessoas que atingem a aposentadoria numa eventual mudança na idade da aposentadoria não é afetada por
esses óbitos prematuros. No caso de uma mudança, nos dias de hoje, de 55 para 65 anos, por exemplo, o número de
pessoas que se aposentam diminuiria 11% nos bairros ricos e 34% nos bairros pobres.
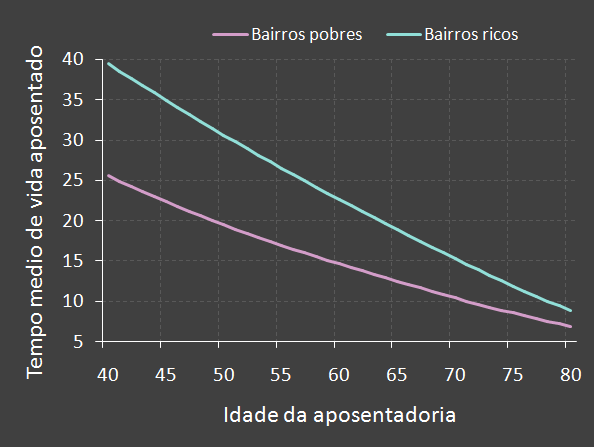 Outro indicador interessante a respeito desse tema é o tempo médio de vida das pessoas após atingirem
a aposentadoria. Esse tempo é maior do que seria esperado ao subtrair a idade de aposentadoria
da expectativa de vida pois, como vimos no parágrafo anterior, grande parte dos residentes em bairros pobres
falecem com idades mais baixas, antes de chegarem a aposentadoria. Logo, ao considerarmos apenas as pessoas
que chegaram na aposentadoria, esse tempo calculado fica bem maior.
Outro indicador interessante a respeito desse tema é o tempo médio de vida das pessoas após atingirem
a aposentadoria. Esse tempo é maior do que seria esperado ao subtrair a idade de aposentadoria
da expectativa de vida pois, como vimos no parágrafo anterior, grande parte dos residentes em bairros pobres
falecem com idades mais baixas, antes de chegarem a aposentadoria. Logo, ao considerarmos apenas as pessoas
que chegaram na aposentadoria, esse tempo calculado fica bem maior.
O gráfico ao lado mostra o número de anos vividos \(V_g(t_A)\) após o início da aposentadoria, em função da idade de início. Ela foi calculada pela fórmula: $$ V_g(t_A) = \frac{1}{A_g(t_A)}\sum_{c,t>t_A} t f_{g,c}(t) - t_A.$$ O tempo médio de vida após a aposentadoria iniciada aos 55 e 65 anos é de 26,5 e 19,6 para residentes dos bairros ricos e 16,9 e 12,9 para residentes dos bairros pobres, respectivamente.
Vale a pena relembrar que essa análise é bastante simplificada se comparada com cenários reais de mudanças nas regras da previdência. Nós não consideramos diferenças na legislação nem na distribuição de óbitos quanto a homens e mulheres, não consideramos uma possível evolução das distribuições com o tempo, não levamos em conta todas as complexidades da legislação e não ponderamos que diferentes grupos podem ter acesso a mecanismos diferentes de aposentadoria. Entretanto, essa análise serve para mostrar como cada grupo social se relaciona e podem ser afetados de maneiras diferentes por uma eventual reforma.